Matrices Worksheets 1.4: Finding The Inverse of a 2 x 2 Matrix

further maths worksheets
matrices
A worksheet on finding the inverse of 2x2 matrices.
Published

April 30, 2025

Introduction

During the COVID-19 pandemic I created some worksheets based on A Level Maths and Further Maths. I’ve decided to upload these to my blog in case they can be of use.

Finding The Inverse of a 2 x 2 Matrix

  1. For each of the following matrices:
  1. Calculate their determinant.
  2. Find their inverse, if it exists.

  1. \[ \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ \end{pmatrix} \]

  2. \[ \begin{pmatrix} 1 & -1 \\ 6 & 2 \end{pmatrix} \]

  3. \[ \begin{pmatrix} 2 & 0 \\ 3 & -3 \end{pmatrix} \]

  4. \[ \begin{pmatrix} 2 & 3 \\ 5 & 7 \end{pmatrix} \]

  5. \[ \begin{pmatrix} -3 & -1 \\ -2 & 6 \end{pmatrix} \]

  6. \[ \begin{pmatrix} 5 & 7 \\ -4 & 0 \end{pmatrix} \]

  1. For what values of \(k\) does the matrix \[\begin{pmatrix} k & 2k \\ 1 & -k \end{pmatrix} \] have an inverse?

  2. Given the matrices

\[ \text{A} = \begin{pmatrix} 0 & 2 \\ 1 & -6 \end{pmatrix} \] and \[ \text{B} = \begin{pmatrix} -4 & -3 \\ 7 & 4 \end{pmatrix} \] find:

  1. \(\text{A}^{-1}\)

  2. \(\text{B}^{-1}\)

  3. \(\text{A}^{-2}\text{B}\)

  4. \(\text{(AB)}^{-1}\)

  5. \(\text{(BA)}^{-1}\)

  1. By considering the inverse of the matrix \[\begin{pmatrix} a & b \\ c & d \end{pmatrix},\] derive the general formula for the inverse of a 2 x 2 matrix, stating under which condition this result holds.

  1. Prove that for any two invertible matrices A and B, \(\text{(AB)}^{-1} = \text{B}^{-1}\text{A}^{-1}\).

  1. Find the inverse of the general rotation matrix R for a rotation of θ degrees anticlockwise about the origin. \[\text{R} = \begin{pmatrix} \cos{θ} & -\sin{θ} \\ \sin{θ} & \cos{θ} \end{pmatrix}.\] What does the matrix \(\text{R}^{-1}\) represent geometrically.

    1. Prove that for an invertible 2 x 2 matrix \[\text{A} = \begin{pmatrix} a & b \\ c & d \end{pmatrix},\] then
      \[ \text{det(A}^{-1}) = \frac{1}{\text{det(A)}}.\]
  1. By considering the fact that for an invertible n x n matrix \(\text{B}\), \[\text{BB}^{-1} =\text{I}\] prove the result in (a) generally for an n x n invertible matrix.

Solutions

1)

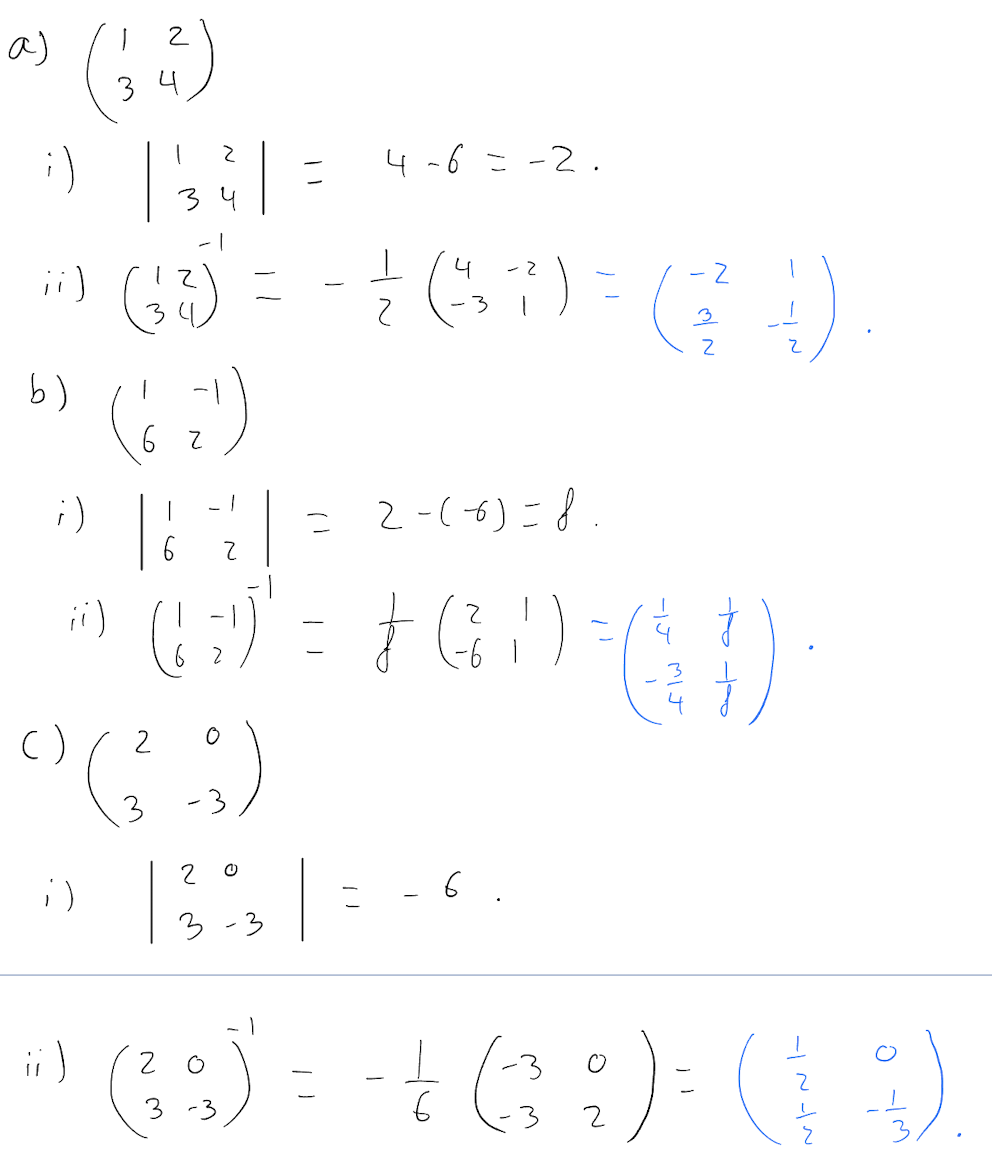
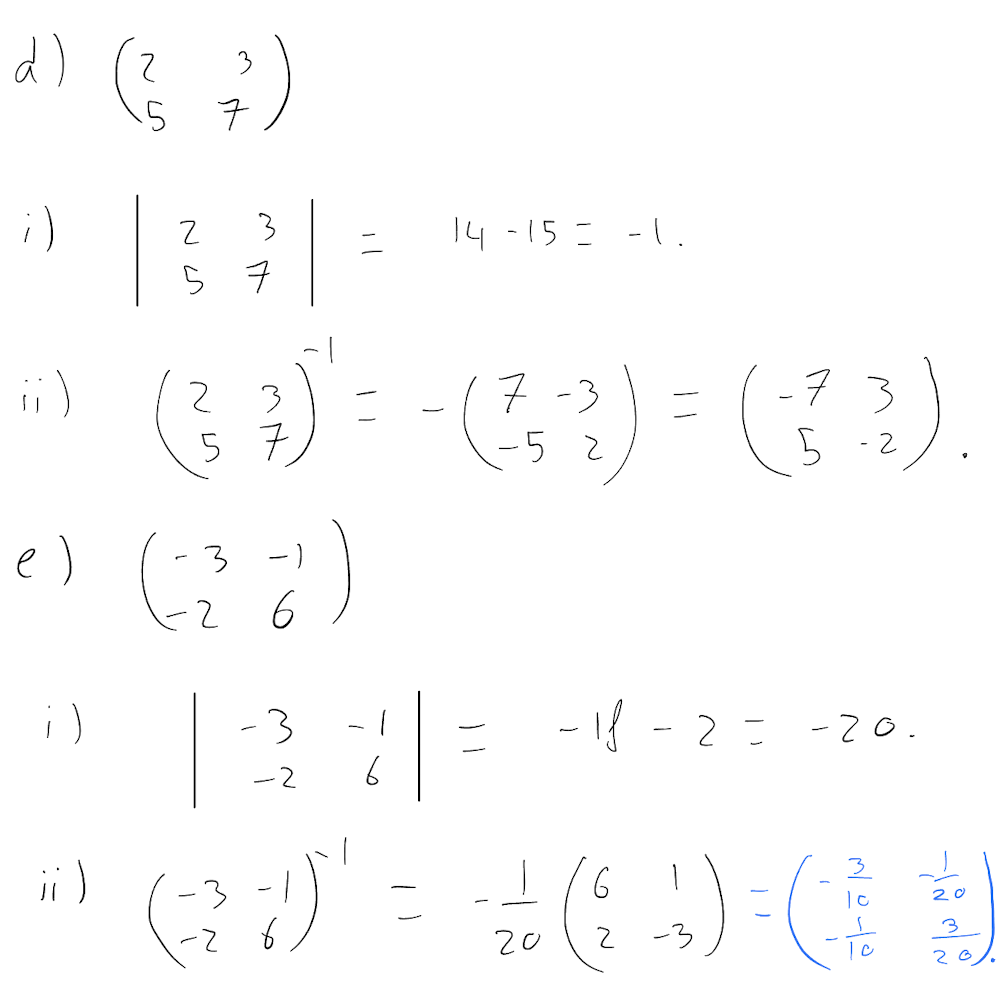
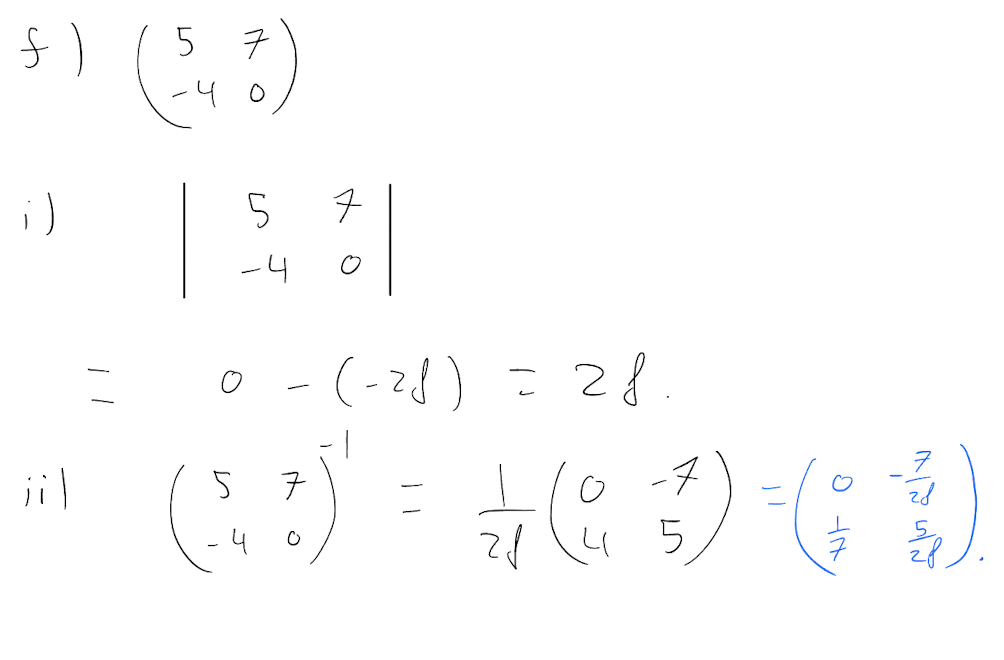
2)

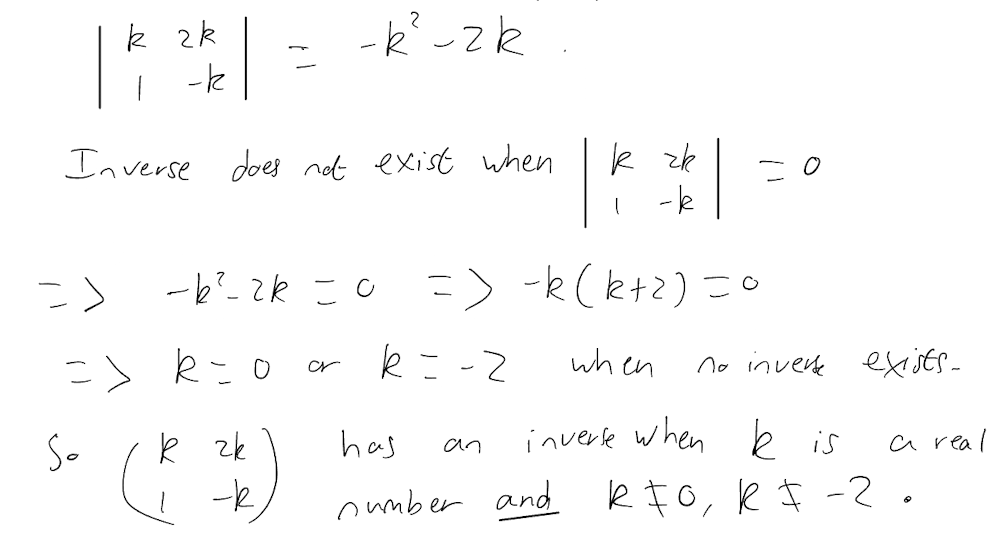
3)

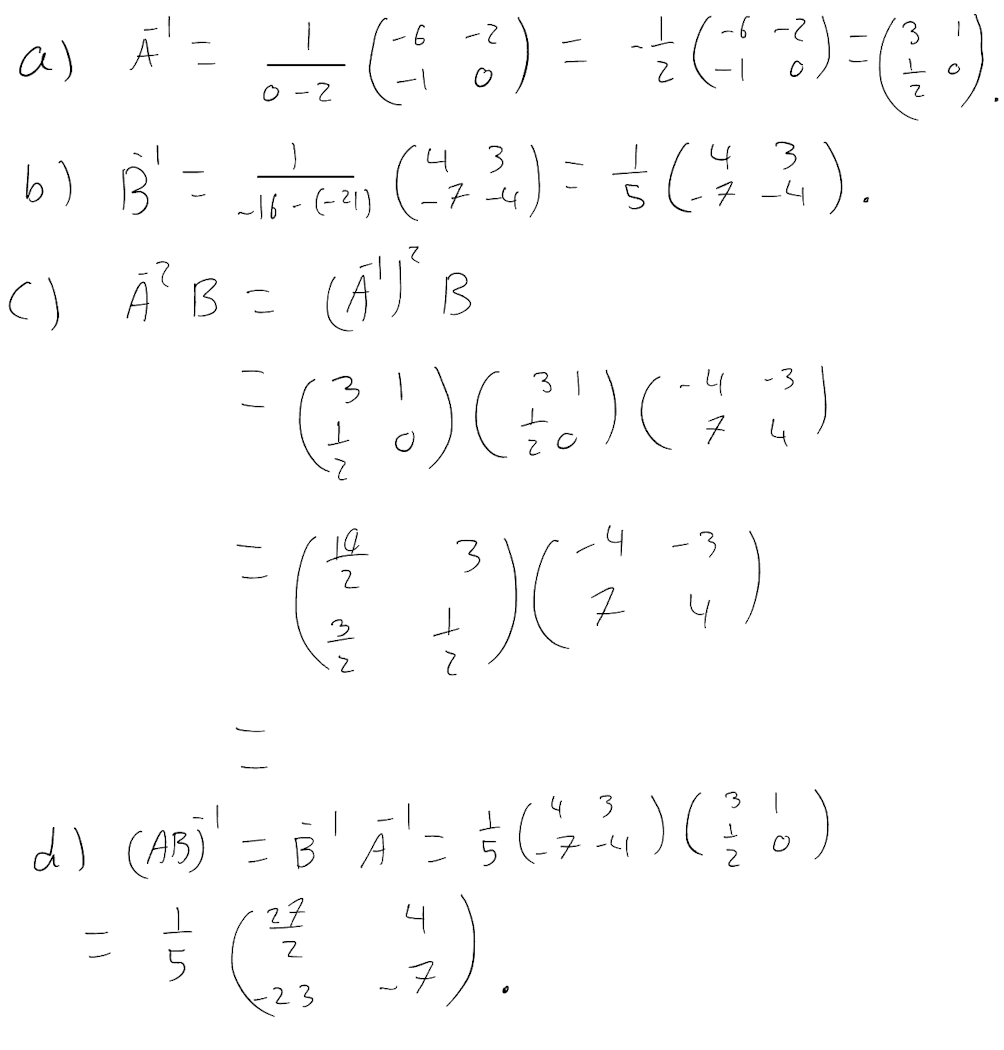
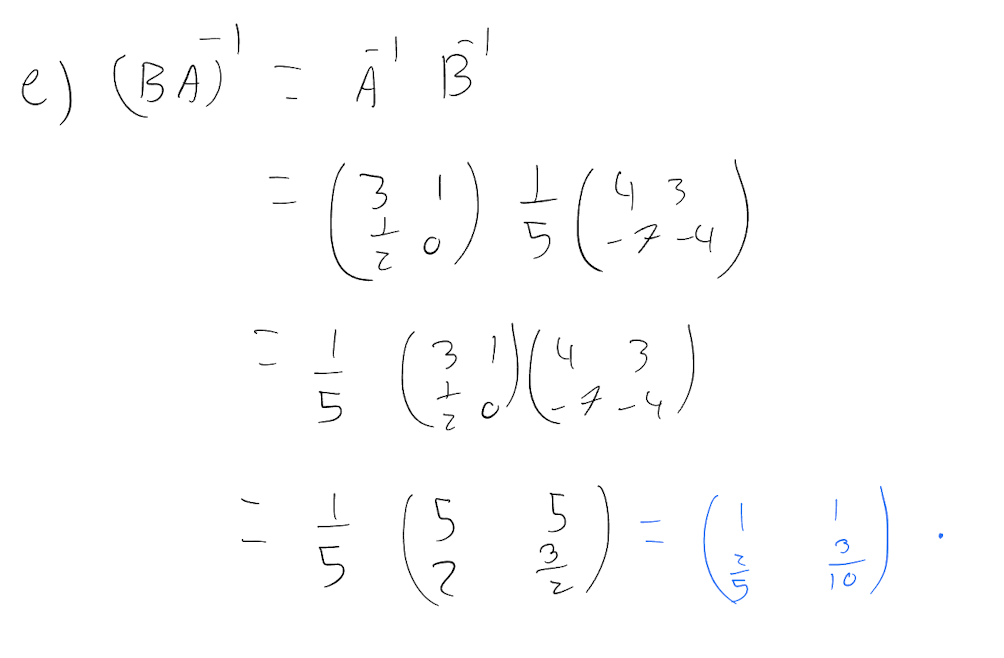
4)

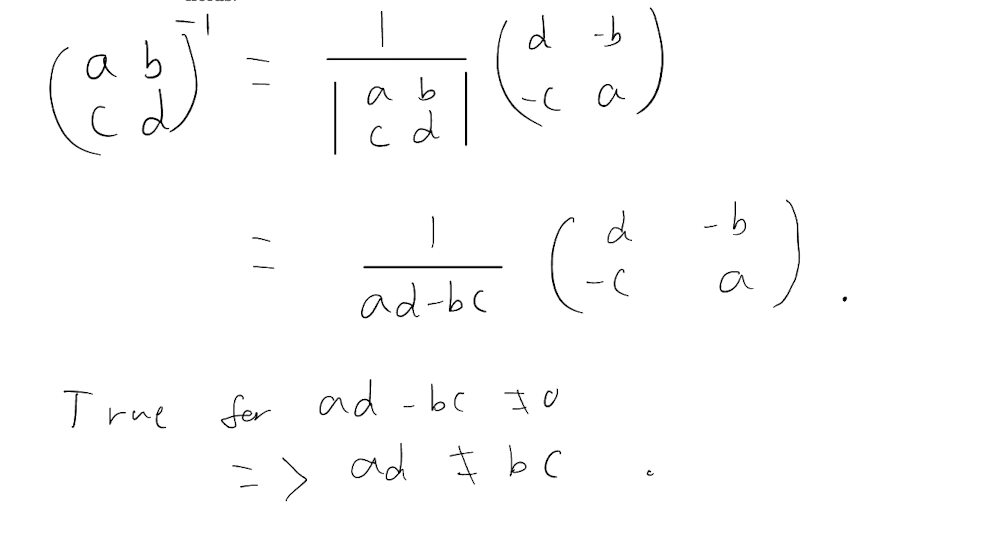
5)

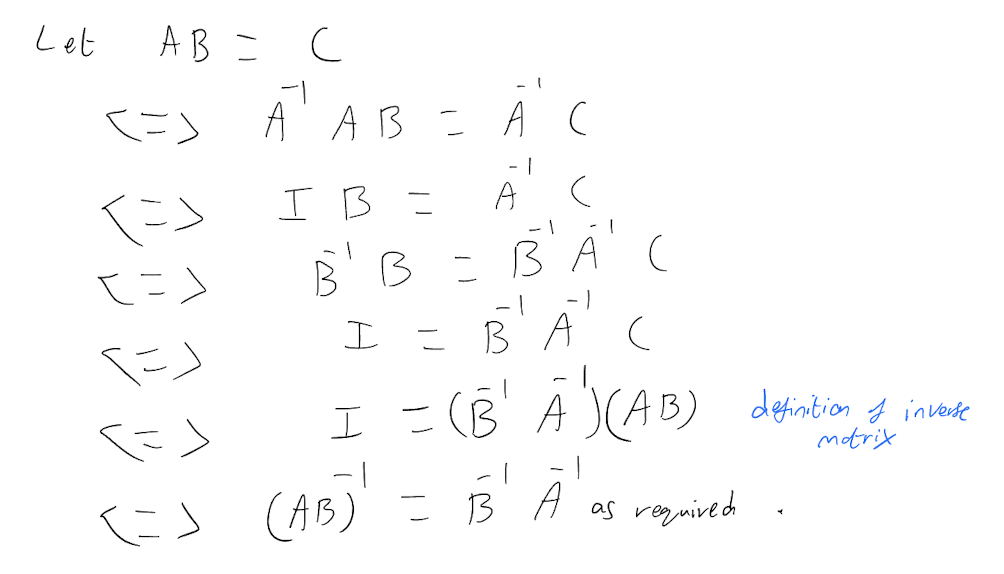
6)

7)