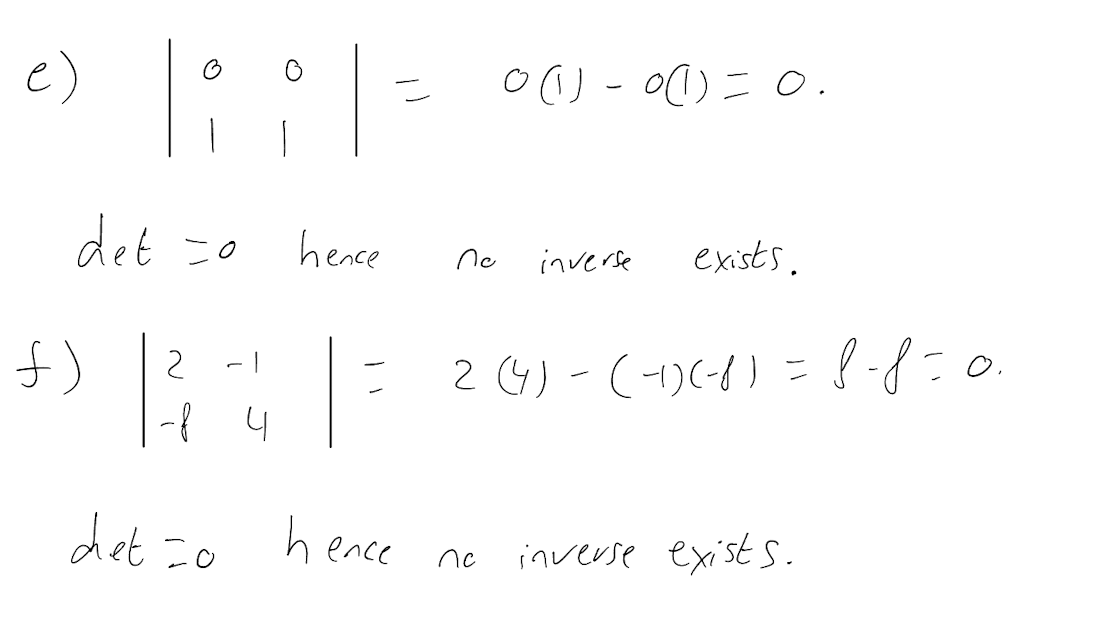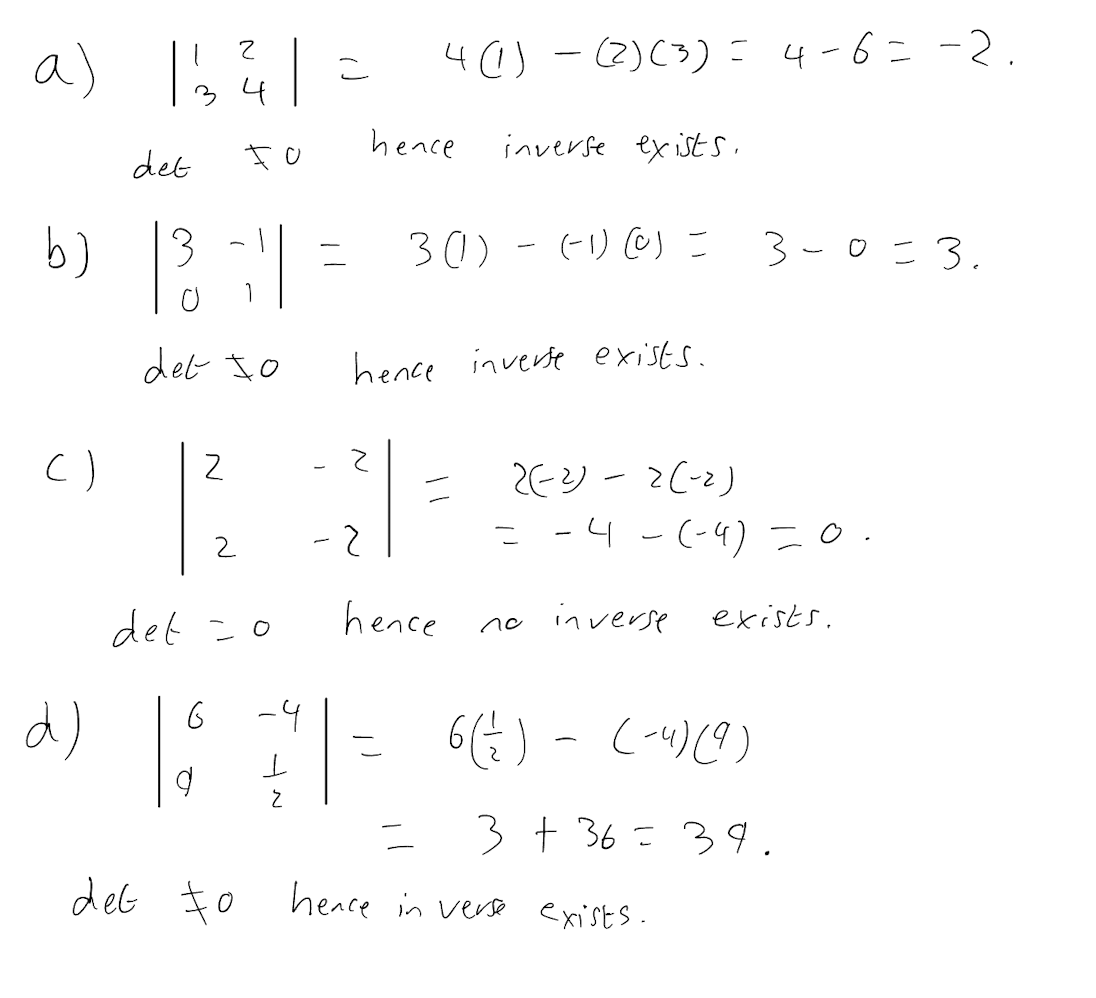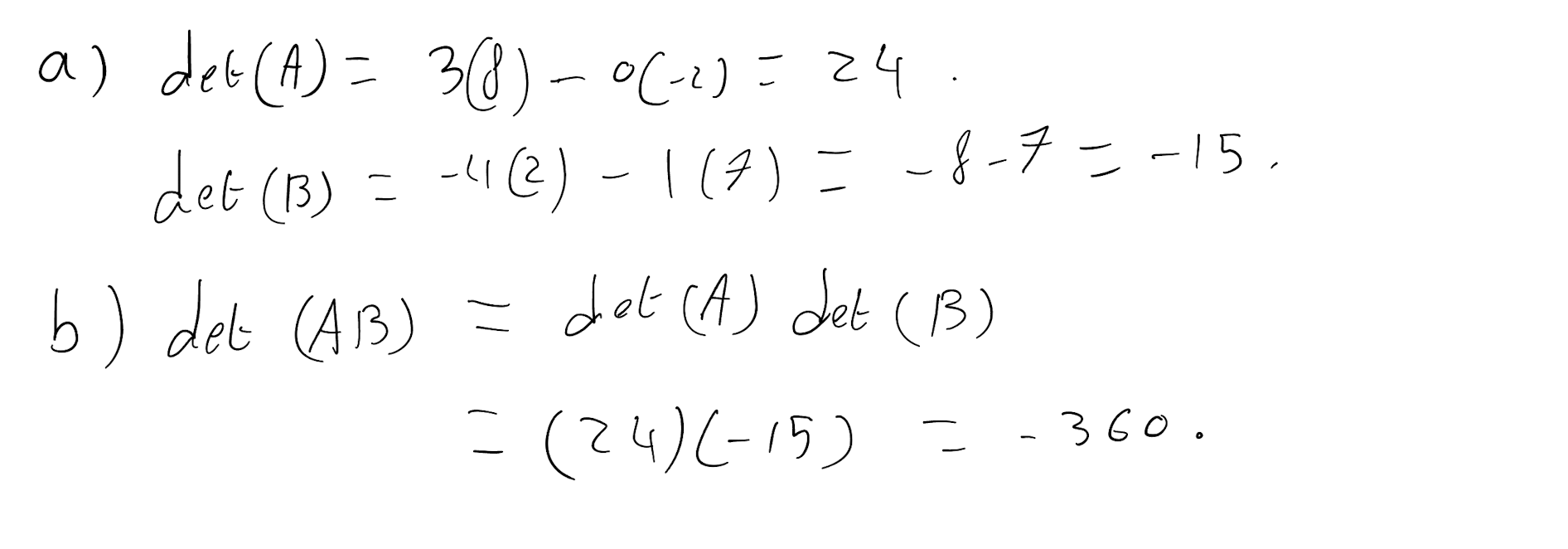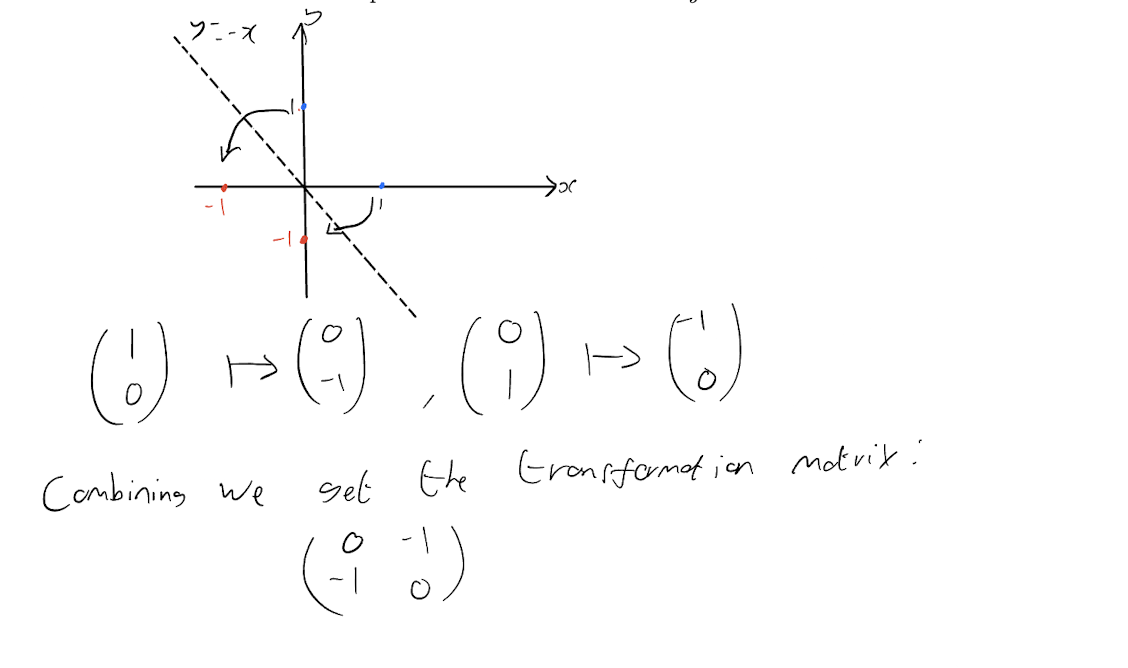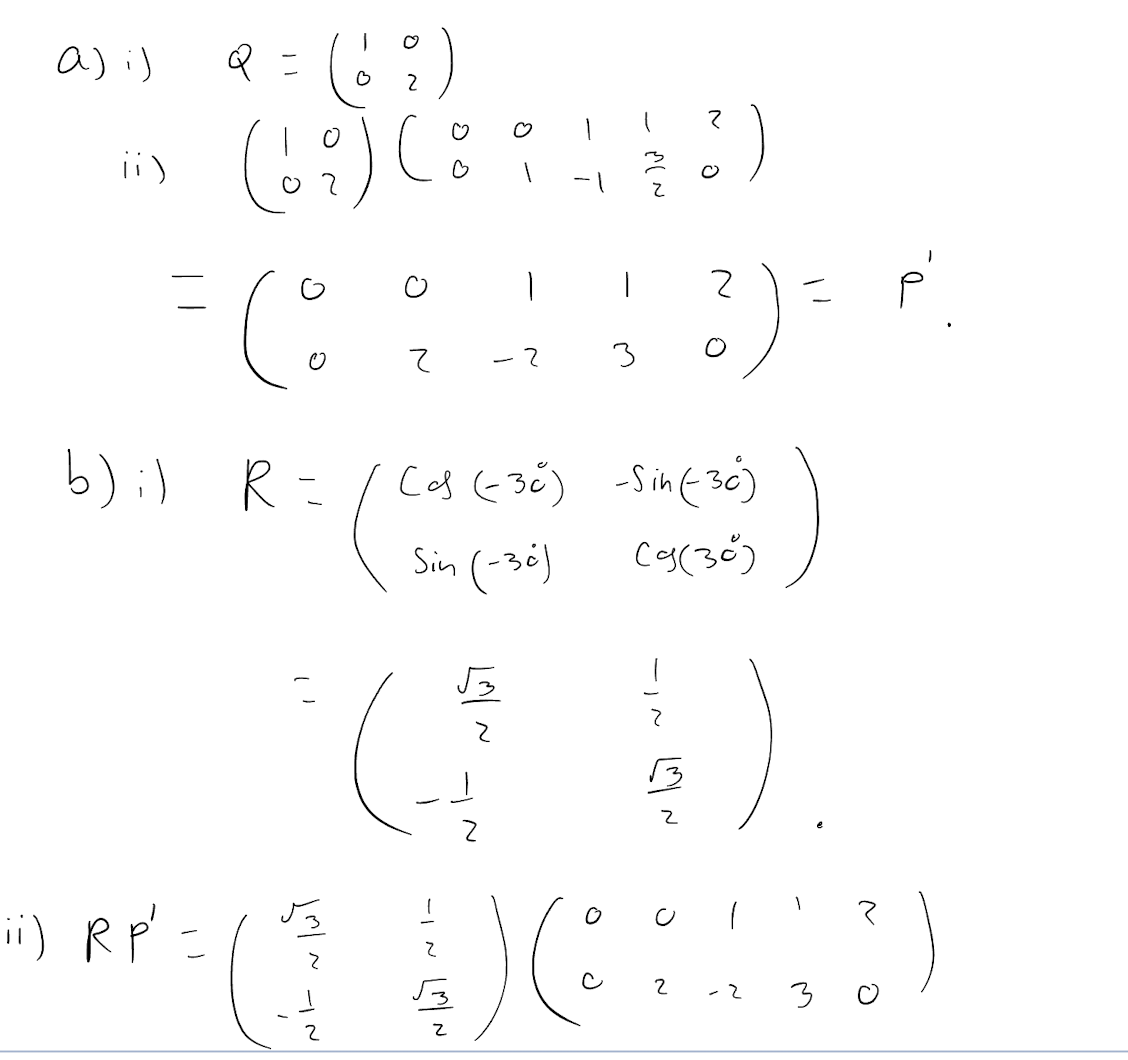Matrices Worksheets 1.3: Determinants and Transformations

A worksheet on finding determinants of 2x2 matrices.

Introduction

During the COVID-19 pandemic I created some worksheets based on A Level Maths and Further Maths. I’ve decided to upload these to my blog in case they can be of use.

Determinants and Transformations

1. For each of the following matrices, find their determinant and state if an inverse matrix will exist.

1. \[ \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ \end{pmatrix} \]

2. \[ \begin{pmatrix} 3 & -1 \\ 0 & 1 \end{pmatrix} \]

3. \[ \begin{pmatrix} 2 & -2 \\ 2 & -2 \end{pmatrix} \]

4. \[ \begin{pmatrix} 6 & -4 \\ 9 & \frac{1}{2} \end{pmatrix} \]

5. \[ \begin{pmatrix} 0 & 0 \\ 1 & 1 \end{pmatrix} \]

6. \[ \begin{pmatrix} 2 & -1 \\ -8 & 4 \end{pmatrix} \]

   ---

2. Given the matrices \[ \text{A} = \begin{pmatrix} 3 & -2 \\ 0 & 8 \end{pmatrix} \] and

\[ \text{B} = \begin{pmatrix} -4 & 7 \\ 1 & 2 \end{pmatrix}. \]

1. Calculate \(\text{det(A)}\) and \(\text{det(B)}\)

2. Without calculating the product \(\text{AB}\), find \(\text{det(AB)}\)

   ---

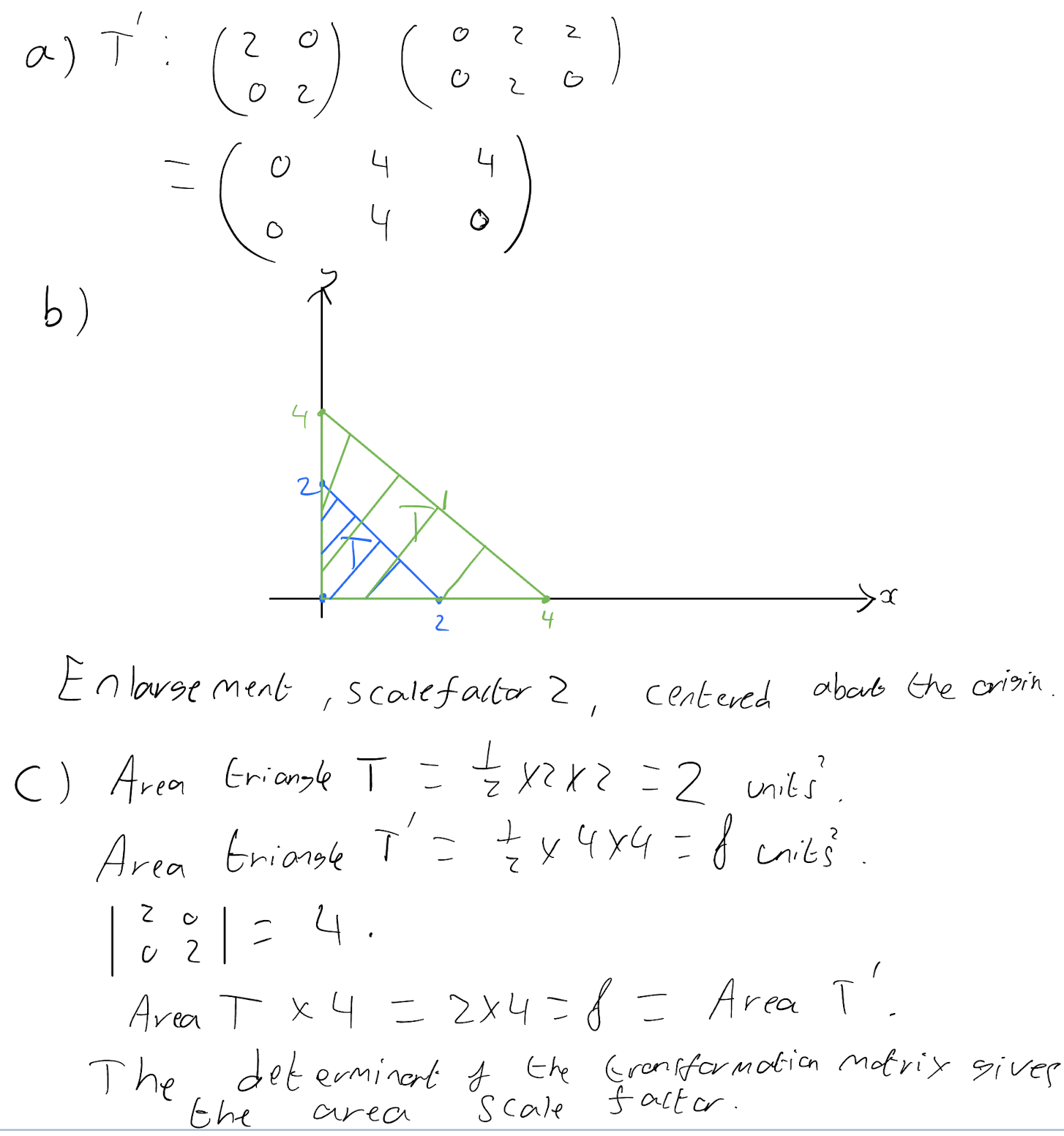
3. A triangle T with points A(0,0), B(2,2) and C(2,0) is acted on by a transformation matrix \[ \text{R} = \begin{pmatrix} 2 & 0 \\ 0 & 2 \end{pmatrix}\]

1. Find T’, the image of the triangle T under the matrix R.

2. Describe the transformation given by the matrix T.

3. Calculate the determinant of the matrix R. How does this value relate to the transformation.

   ---

4. By considering the image of the unit square under the following matrices, describe the transformation they represent.

1. \[\begin{pmatrix} \frac{1}{2} & 0 \\ 0 & 2 \end{pmatrix}\]

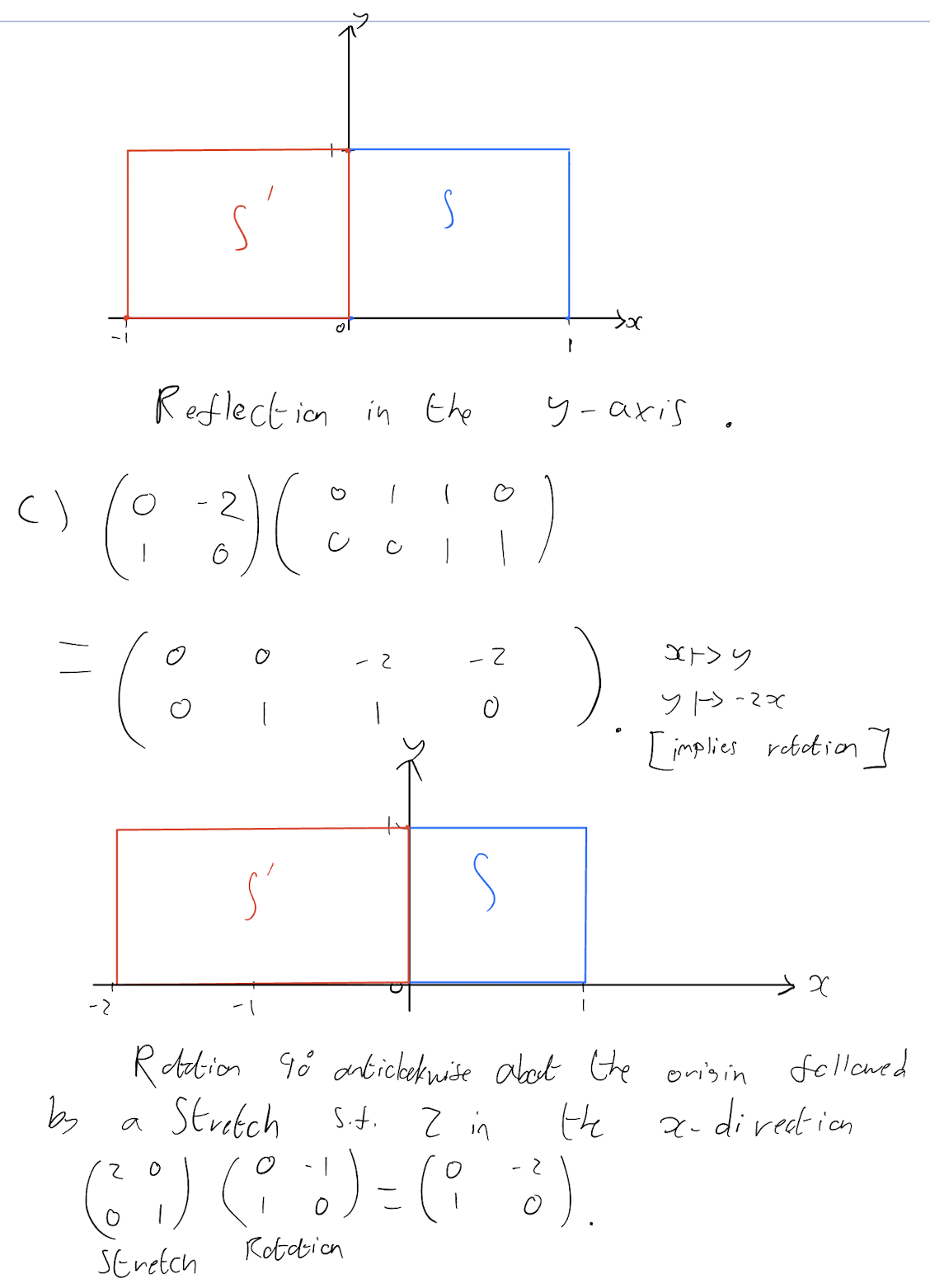
2. \[\begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}\]

3. \[\begin{pmatrix} 0 & -2 \\ 1 & 0 \end{pmatrix}\]

   ---

5. By considering the effect on the unit vectors \[\begin{pmatrix} 1 \\ 0 \end{pmatrix}\] and \[\begin{pmatrix} 0 \\ 1 \end{pmatrix},\] find the 2 x 2 matrix which represents a reflection in the line \(y = -x\).

   ---

6. Find the 2 x 2 matrix which represents a rotation of 120° anticlockwise about the origin.

   ---

7. An irregular pentagon has coordinate matrix \[P = \begin{pmatrix} 0 & 0 & 1 & 1 & 2 \\ 0 & 1 & -1 & \frac{3}{2} & 0 \end{pmatrix}.\]

1. 1. Find the matrix Q which represents a stretch, scale factor 2, in the y-direction.

2. Apply this matrix to P.

2. 1. Find the matrix R which represents a rotation of 30° clockwise about the origin.

2. Apply this matrix to the results of (a) ii. .

3. 1. Find the matrix S which represents the effect of matrix Q followed by R.

2. Apply this to P and confirm the resulting matrix is identical to the result in (b) ii. .

Solutions

1. 

2. 
3. 
4. 
5. 
6. 
7.