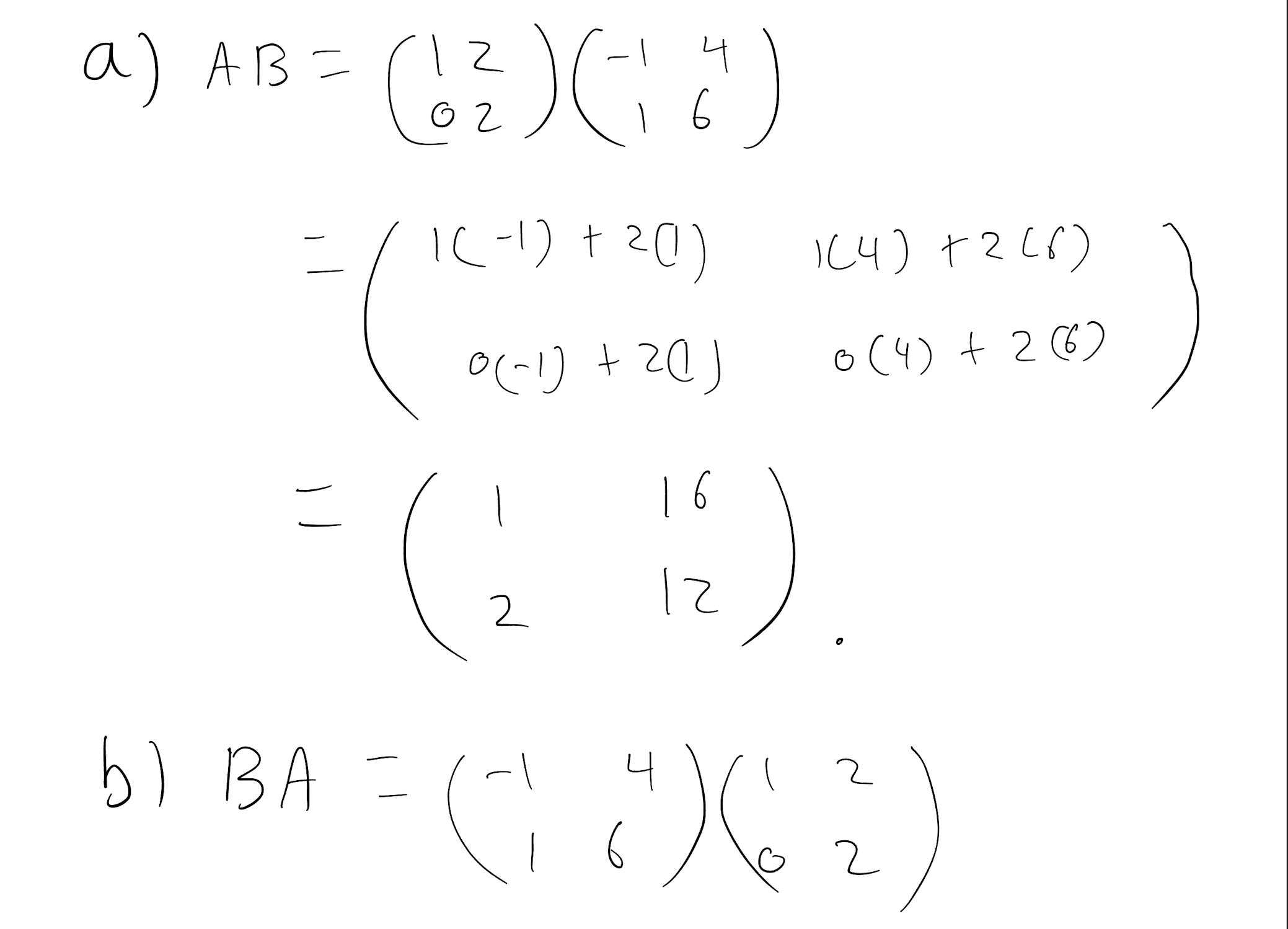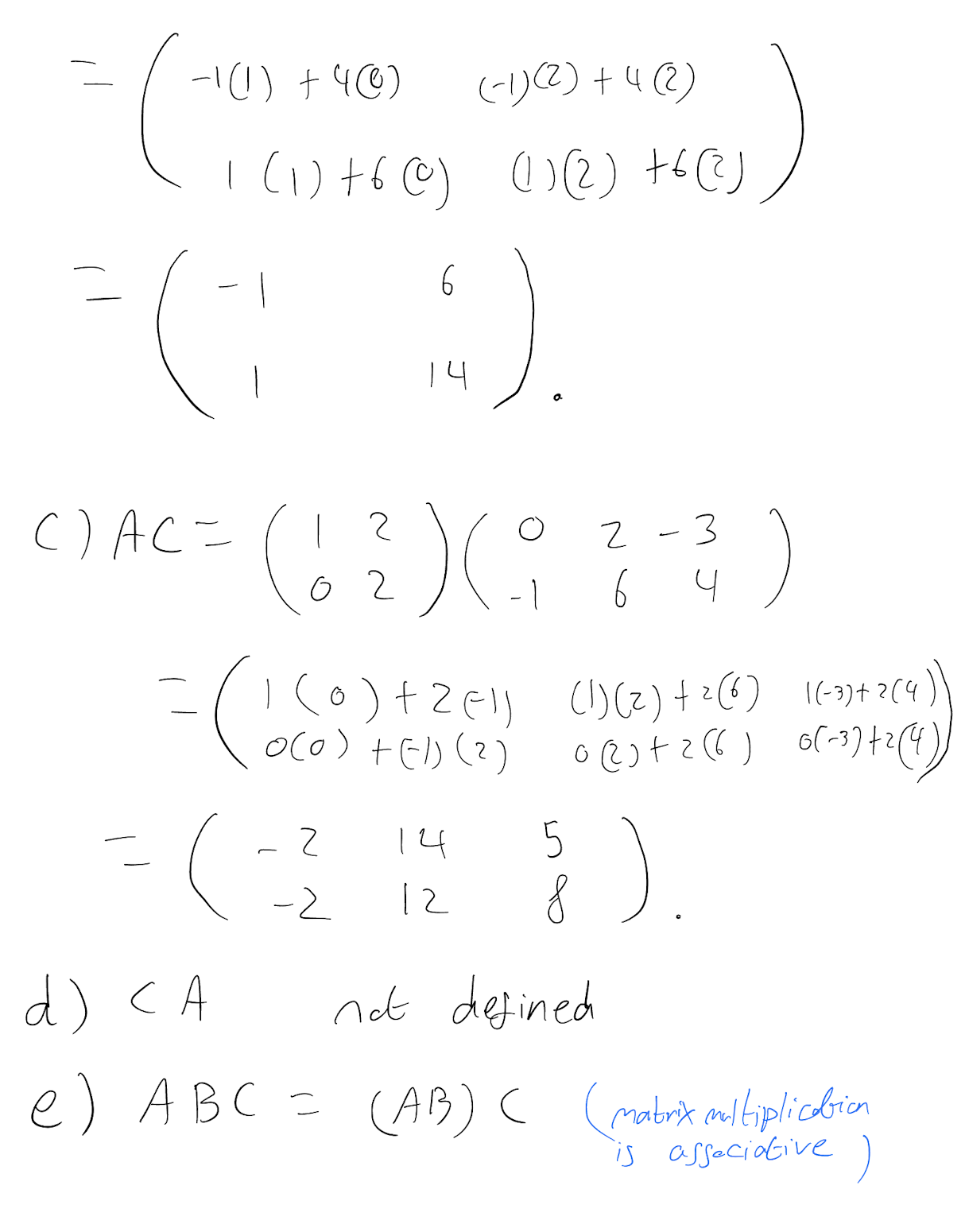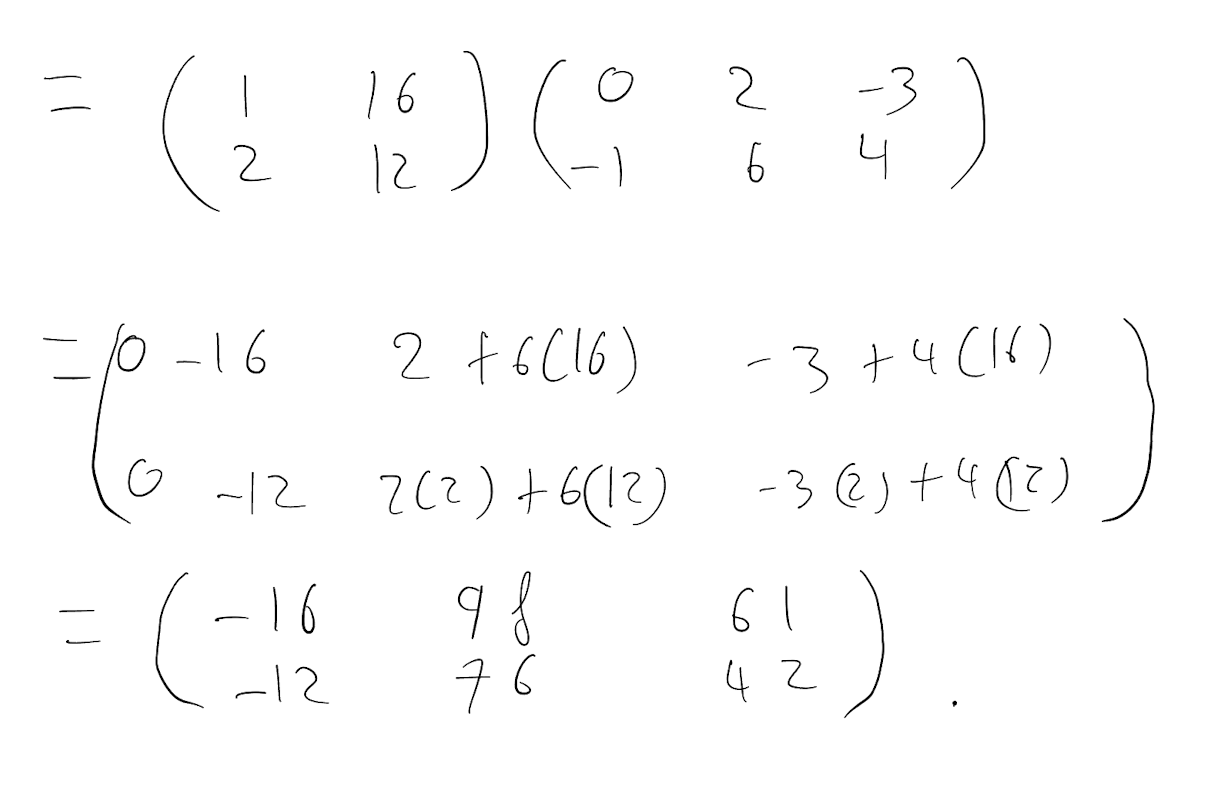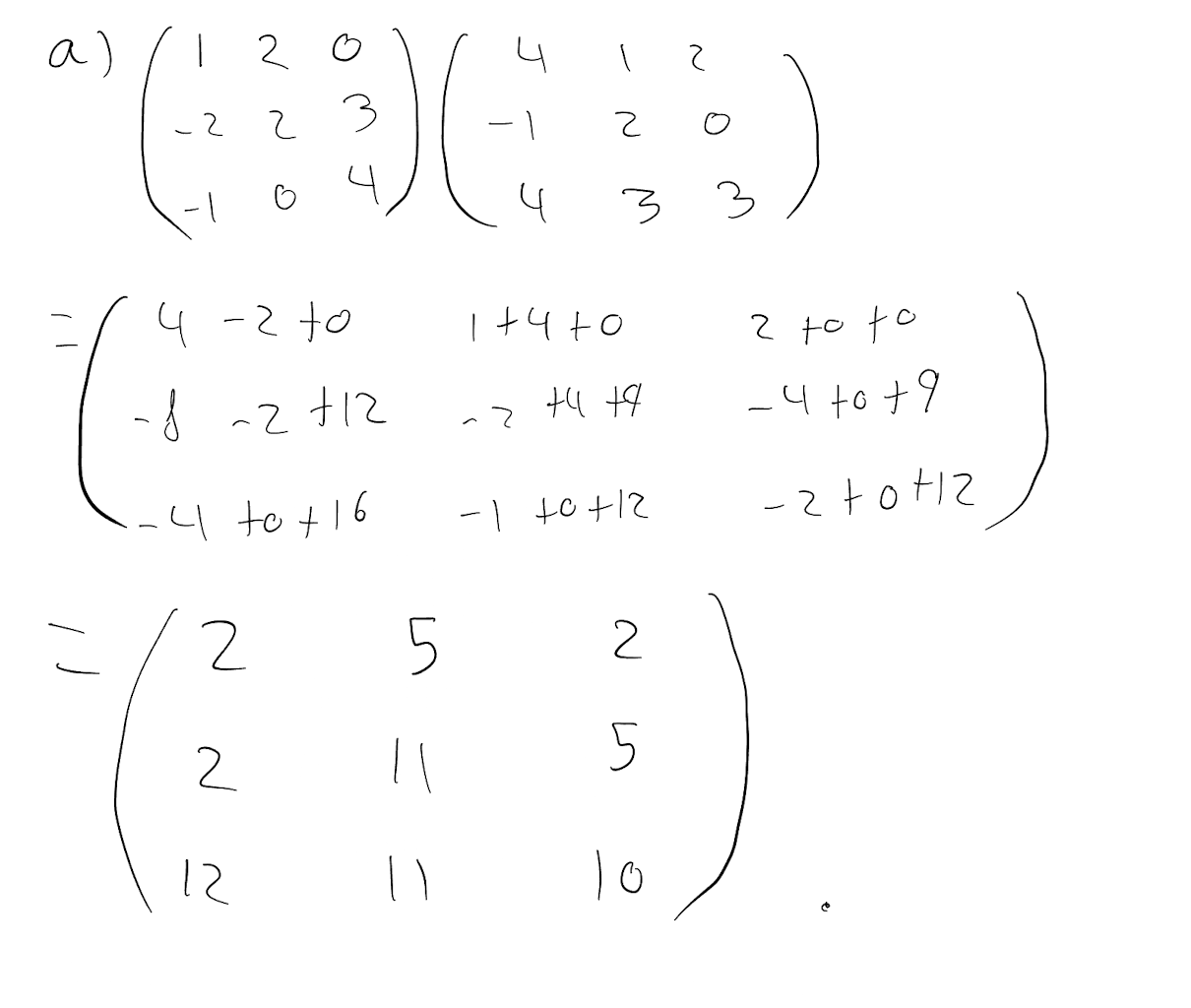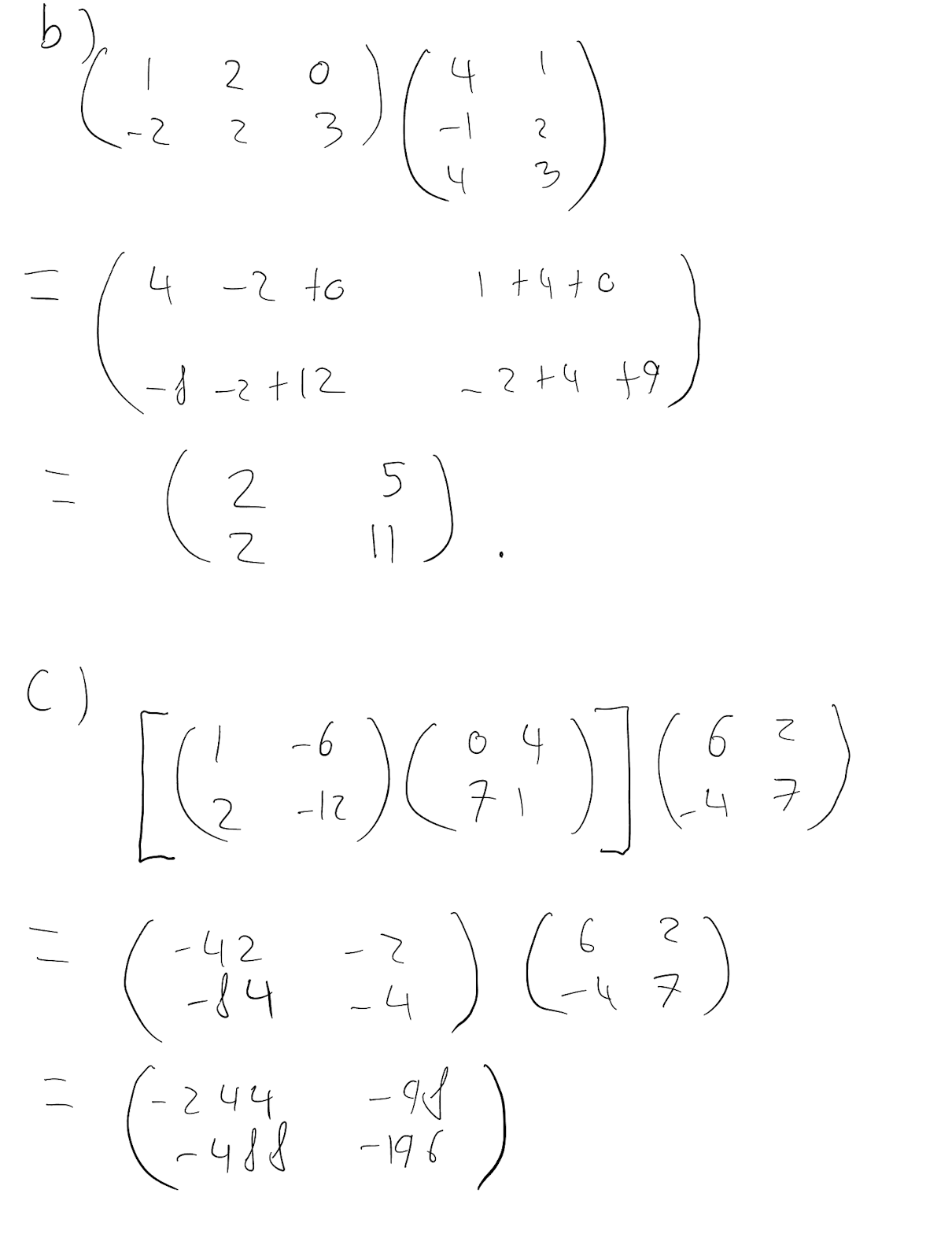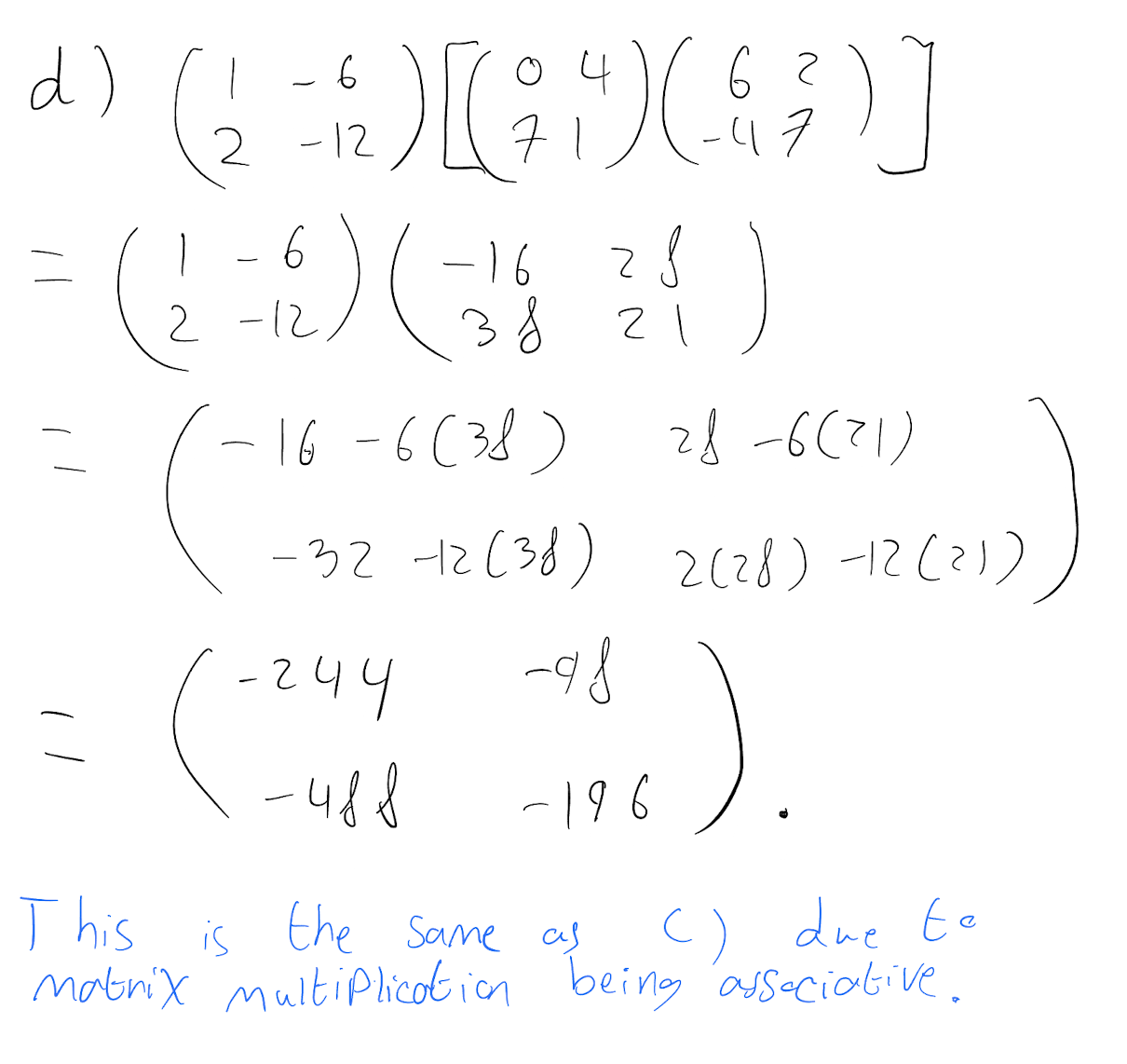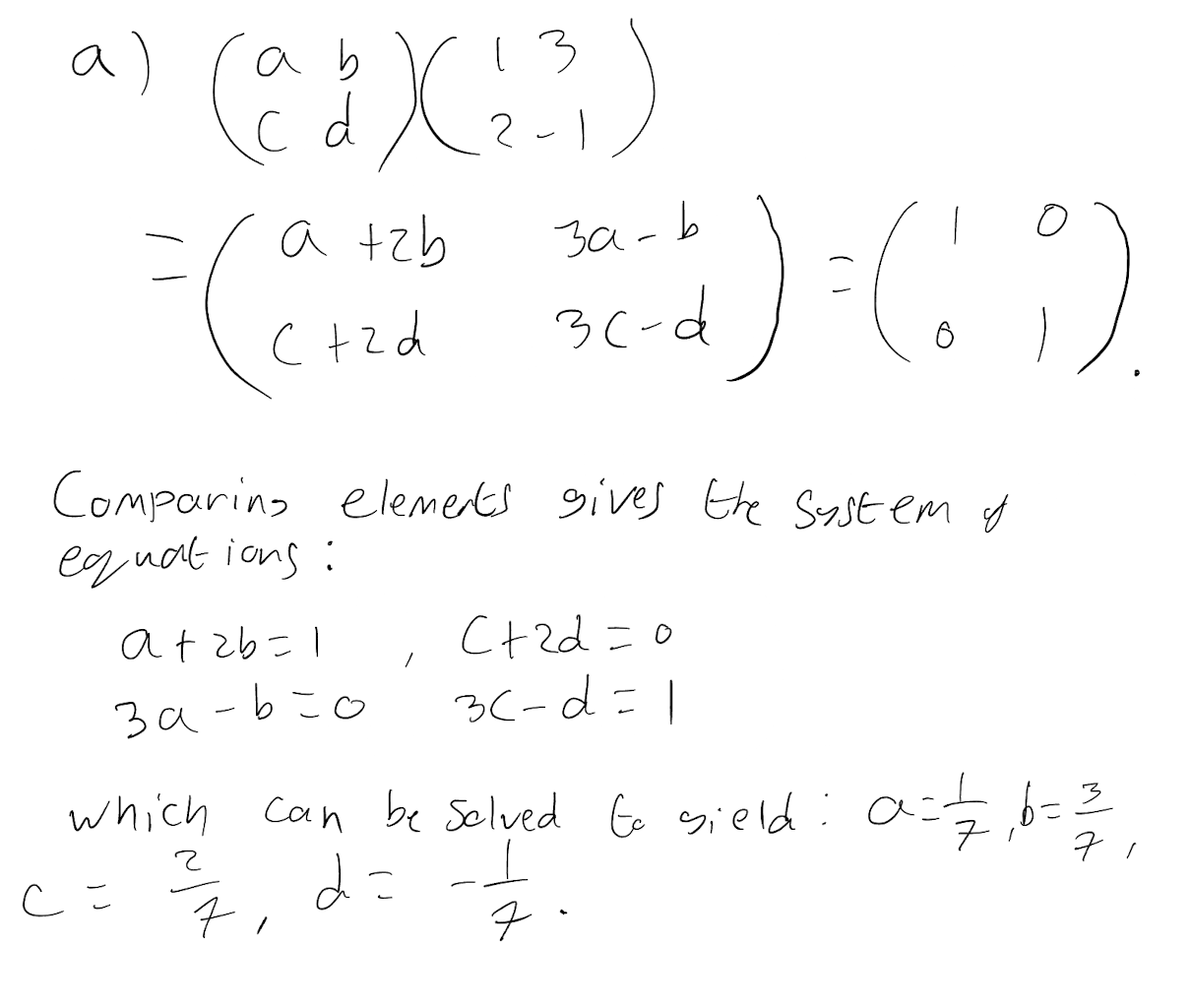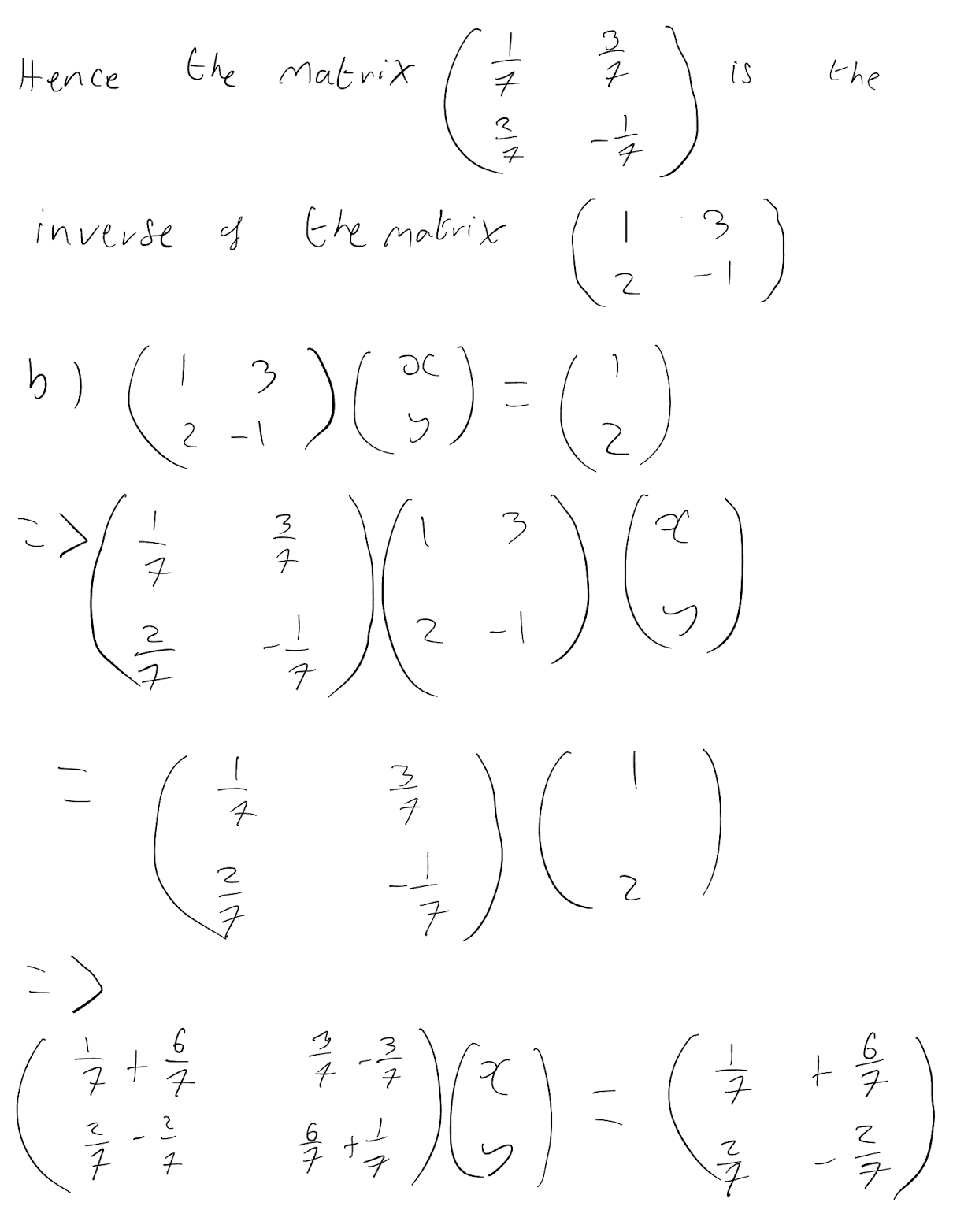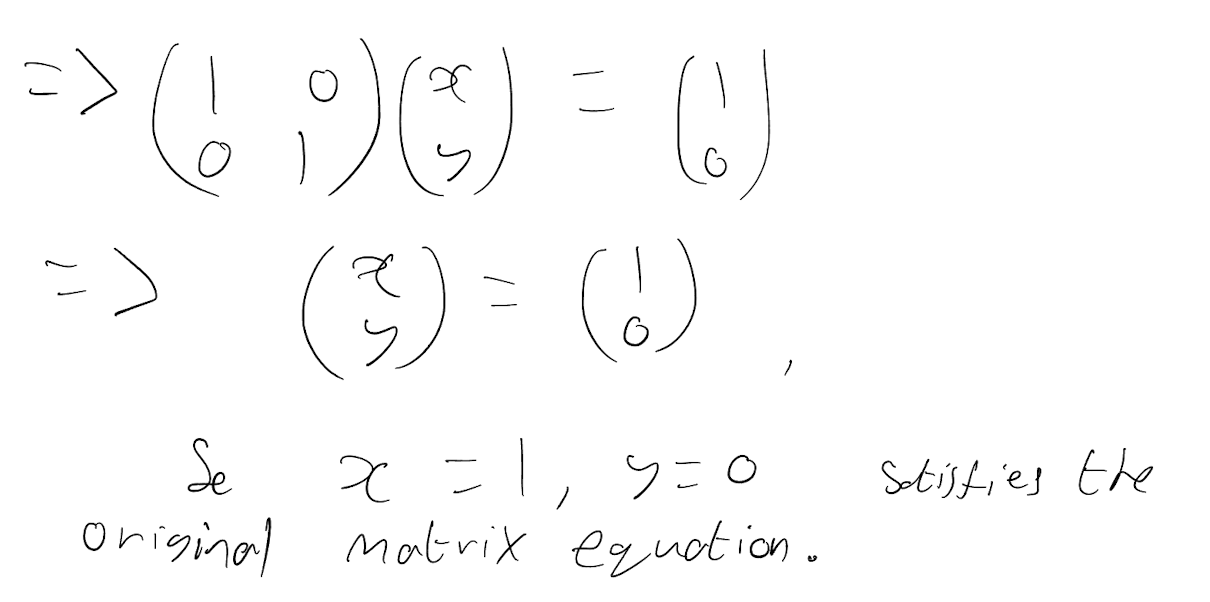Matrices Worksheets 1.2: Matrix Multiplication
Introduction
During the COVID-19 pandemic I created some worksheets based on A Level Maths and Further Maths. I’ve decided to upload these to my blog in case they can be of use.
Matrix Multiplication
Given the matrices:
A = \[ \begin{pmatrix} 1 & 2 \\ 0 & 2 \\ \end{pmatrix} \]
B = \[ \begin{pmatrix} -1 & 4 \\ 1 & 6 \end{pmatrix} \]
C = \[ \begin{pmatrix} 0 & 2 & -3\\ -1 & 6 & 4\\ \end{pmatrix} \]
Calculate, where defined, the following matrix products.
AB
BA
AC
CA
ABC
- Find each of the following matrix products.
\[ \begin{pmatrix} 1 & 2 & 0 \\ -2 & 2 & 3 \\ -1 & 0 & 4 \end{pmatrix}\begin{pmatrix} 4 & 1 & 2 \\ -1 & 2 & 0 \\ 4 & 3 & 3 \end{pmatrix} \]
\[ \begin{pmatrix} 1 & 2& 0\\ -2 & 2 & 3 \\ \end{pmatrix} \begin{pmatrix} 4 & 1\\ -1 & 2 \\ 4 & 3 \\ \end{pmatrix} \]
\[ \begin{bmatrix}\begin{pmatrix} 1 & -6\\ 2& -12\\ \end{pmatrix}\begin{pmatrix} 0 & 4\\ 7& 1\\ \end{pmatrix}\end{bmatrix}\begin{pmatrix} 6 & 2\\ -4& 7\\ \end{pmatrix} \]
\[ \begin{pmatrix} 1 & -6\\ 2& -12\\ \end{pmatrix}\begin{bmatrix}\begin{pmatrix} 0 & 4\\ 7& 1\\ \end{pmatrix}\begin{pmatrix} 6 & 2\\ -4& 7\\ \end{pmatrix}\end{bmatrix} \]
- The inverse of a matrix is defined to be the matrix such that (pre or post) multiplying it by the original matrix yields the identity matrix.
By considering the equation \[ \begin{pmatrix} a & b\\ c& d\\ \end{pmatrix}\begin{pmatrix} 1 & 3\\ 2& -1\\ \end{pmatrix} = \begin{pmatrix} 1 & 0\\ 0& 1\\ \end{pmatrix} \] find the inverse of the matrix \[\begin{pmatrix} 1 & 3\\ 2& -1\\ \end{pmatrix} \] (you do not need to worry about checking by post multiplying).
Pre multiply both side of the matrix equation \[ \begin{pmatrix} 1 & 3\\ 2& -1\\ \end{pmatrix}\begin{pmatrix} x\\ y\\ \end{pmatrix} = \begin{pmatrix} 1\\ 2\\ \end{pmatrix} \] by your result in (a) to obtain the values of \(x\) and \(y\) which satisfy the matrix equation.